Page 213 - Physics

Work, energy and power

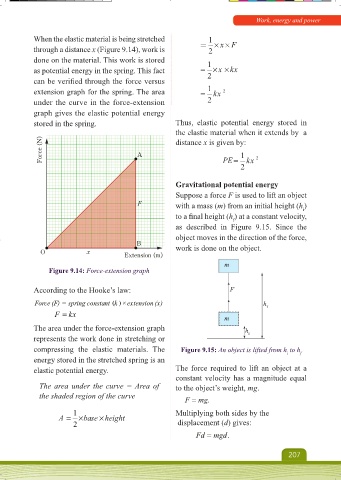
When the elastic material is being stretched = ×x×F
1
through a distance x (Figure 9.14), work is 2
done on the material. This work is stored 1
x kx
as potential energy in the spring. This fact  
2
can be verifi ed through the force versus
extension graph for the spring. The area  1 kx 2
under the curve in the force-extension 2
graph gives the elastic potential energy
stored in the spring. Thus, elastic potential energy stored in
the elastic material when it extends by a
Force (N) A distance x is given by: 2
1
PE 
2 kx

Gravitational potential energy
Suppose a force F is used to lift an object
F with a mass (m) from an initial height (h )
i
to a fi nal height (h ) at a constant velocity,
f
as described in Figure 9.15. Since the
object moves in the direction of the force,
B work is done on the object.
O x
Extension (m)
m
Figure 9.14: Force-extension graph

According to the Hooke’s law: F
Force (F) = spring constant ()k ×extension (x) h
f
F = kx m
The area under the force-extension graph h
represents the work done in stretching or i
compressing the elastic materials. The Figure 9.15: An object is lifted from h to h f
i
energy stored in the stretched spring is an
elastic potential energy. The force required to lift an object at a
constant velocity has a magnitude equal
The area under the curve = Area of to the object’s weight, mg.
the shaded region of the curve F = mg.

1 Multiplying both sides by the
A  base height
2 displacement (d) gives:
Fd = mgd.

207

Physics Form 1 Final.indd 207 16/10/2024 20:58