Page 25 - Computer_Science_F5

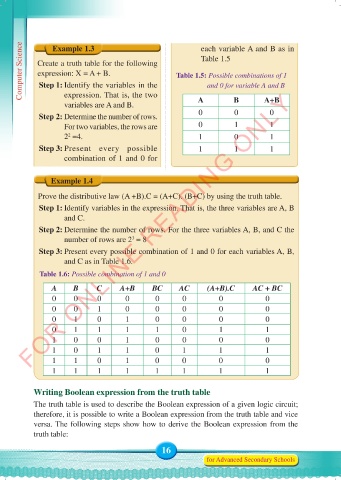
Computer Science Create a truth table for the following Table 1.5: Possible combinations of 1
each variable A and B as in
Example 1.3
Table 1.5
expression: X = A + B.
Step 1: Identify the variables in the

and 0 for variable A and B
FOR ONLINE READING ONLY
expression. That is, the two
variables are A and B. A B A+B
Step 2: Determine the number of rows. 0 0 0
For two variables, the rows are 0 1 1
2 =4. 1 0 1
2
Step 3: Present every possible 1 1 1
combination of 1 and 0 for

Example 1.4

Prove the distributive law (A +B).C = (A+C). (B+C) by using the truth table.
Step 1: Identify variables in the expression. That is, the three variables are A, B
and C.
Step 2: Determine the number of rows. For the three variables A, B, and C the
number of rows are 2 = 8
3
Step 3: Present every possible combination of 1 and 0 for each variables A, B,
and C as in Table 1.6.

Table 1.6: Possible combination of 1 and 0
A B C A+B BC AC (A+B).C AC + BC
0 0 0 0 0 0 0 0
0 0 1 0 0 0 0 0
0 1 0 1 0 0 0 0
0 1 1 1 1 0 1 1
1 0 0 1 0 0 0 0
1 0 1 1 0 1 1 1
1 1 0 1 0 0 0 0
1 1 1 1 1 1 1 1

Writing Boolean expression from the truth table
The truth table is used to describe the Boolean expression of a given logic circuit;
therefore, it is possible to write a Boolean expression from the truth table and vice
versa. The following steps show how to derive the Boolean expression from the
truth table:

16
for Advanced Secondary Schools

Computer Science Form 5.indd 16 23/07/2024 12:32