Page 161 - Mathematics

9. Two bicycles, one travelling at 3 m/s faster than the other bicycle start
at the same time from the same point. Formulate a linear equation that
represent this scenario. Use table of values to draw the graph of the
equation formulated.
10. A bread is made using 500 g of wheat flour and 100 g of sugar. If the Tanzania Institute of Education
total cost of the two items is Tshs 800;
(a) write a linear equation that represent the cost of the items.
(b) draw the graph of the line in (a).

Solving linear simultaneous equations graphically
Solving linear simultaneous equations graphically helps to realize and understand
the relationships between variables and their solutions. Engage in Activity 6.4 to
learn this relationship.

Activity 6.4: Recognising the point of intersection of two linear
equations

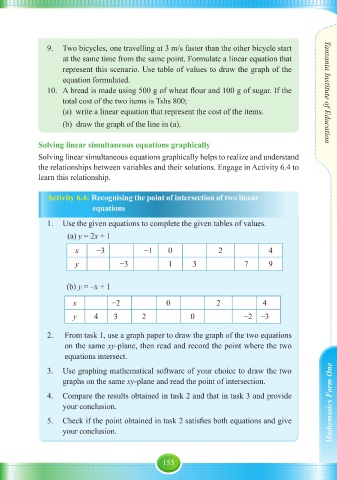
1. Use the given equations to complete the given tables of values.
(a) y = 2x + 1

x −3 −1 0 2 4

y −3 1 3 7 9

(b) y = –x + 1

x −2 0 2 4
y 4 3 2 0 −2 −3

2. From task 1, use a graph paper to draw the graph of the two equations
on the same xy-plane, then read and record the point where the two
equations intersect.
3. Use graphing mathematical software of your choice to draw the two
graphs on the same xy-plane and read the point of intersection.

4. Compare the results obtained in task 2 and that in task 3 and provide
your conclusion. Mathematics Form One
5. Check if the point obtained in task 2 satisfies both equations and give
your conclusion.

155

25/10/2024 09:52:02
Mathematics form 1.indd 155
Mathematics form 1.indd 155 25/10/2024 09:52:02