Page 187 - Physics

Linear motion

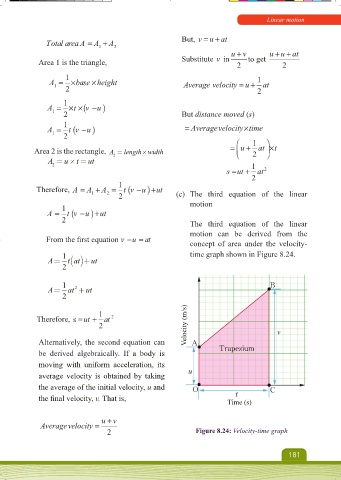
Total areaA  A  1 A 2 But, v u at
uv u u at
Area 1 is the triangle, Substitute v in 2 to get 2

1 1
A  base height Average velocity u 2 at
1
2
1
t
A   vu 

1
2 But distance moved (s)
1
A   tv u   Averagevelocity time
1
2
  u  1 at   t
Area 2 is the rectangle, A = length×width   2  
2
A = u ×t = ut
2 s ut  1 at 2
2
1
Therefore, A  A  1 A  2 2  t v u  ut (c) The third equation of the linear

1 motion
A   t v u  ut
2 The third equation of the linear

motion can be derived from the
u
From the fi rst equation v  at concept of area under the velocity-
1 time graph shown in Figure 8.24.
A= t at ( )+ut
2

1 B
2
A= at +ut
2
1
Therefore, s ut  at 2
2 Velocity (m/s) v

Alternatively, the second equation can A
be derived algebraically. If a body is Trapezium
moving with uniform acceleration, its
average velocity is obtained by taking u
the average of the initial velocity, u and O C
t
the fi nal velocity, v. That is, Time (s)

uv

Averagevelocity 
2 Figure 8.24: Velocity-time graph

181

Physics Form 1 Final.indd 181 16/10/2024 20:58