Page 186 - Physics

Physics for Secondary Schools

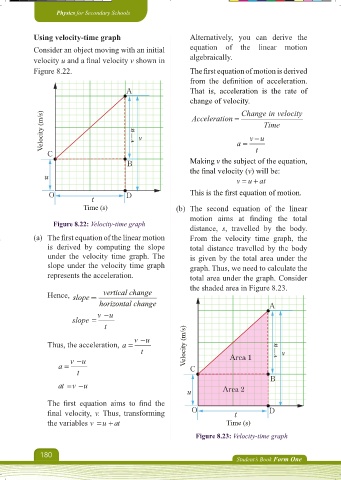
Using velocity-time graph Alternatively, you can derive the
Consider an object moving with an initial equation of the linear motion
velocity u and a fi nal velocity v shown in algebraically.
Figure 8.22. The fi rst equation of motion is derived
from the defi nition of acceleration.
A That is, acceleration is the rate of
change of velocity.
Change in velocity
Velocity (m/s) v-u v Acceleration  vu Time



C a  t
B Making v the subject of the equation,
the fi nal velocity (v) will be:
u v u at

O D This is the fi rst equation of motion.
t
Time (s) (b) The second equation of the linear
motion aims at fi nding the total
Figure 8.22: Velocity-time graph
distance, s, travelled by the body.
(a) The fi rst equation of the linear motion From the velocity time graph, the
is derived by computing the slope total distance travelled by the body
under the velocity time graph. The is given by the total area under the
slope under the velocity time graph graph. Thus, we need to calculate the
represents the acceleration. total area under the graph. Consider
the shaded area in Figure 8.23.
Hence, slope = vertical change
horizontal change A

vu
slope 
t

vu
Thus, the acceleration, a  Velocity (m/s)
t v-u v

vu Area 1
a  C
t
B
v
at  u
u Area 2
The fi rst equation aims to fi nd the
fi nal velocity, v. Thus, transforming O t D
the variables v  Time (s)
u at
Figure 8.23: Velocity-time graph

180
Student’s Book Form One

Physics Form 1 Final.indd 180 16/10/2024 20:58