Page 137 - Mathematics

Equation of a straight line
)
Suppose that two points P( , )xy and Q( ,xy lie on a straight line, then the
1
2
2
1
relationship between x and y coordinates of a point N( , )xy lying on PQ can be
determined. If x ≠ x 2 , then point N will join PQ to form a straight line only if the
1
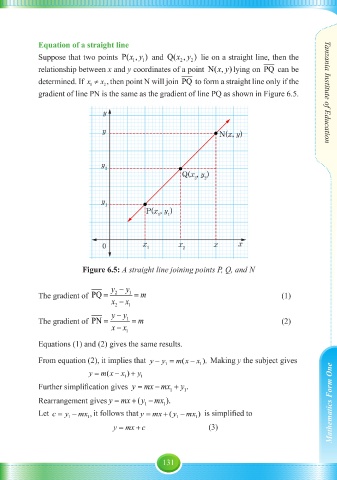
gradient of line PN is the same as the gradient of line PQ as shown in Figure 6.5. Tanzania Institute of Education
y

y
N(x, y)

y
2
Q(x , y )
2 2

y
1
P(x , y )
1 1

0 x 1 x x x
2

Figure 6.5: A straight line joining points P, Q, and N

y − y
The gradient of PQ = 2 1 = m (1)
x − x 1
2
y y−
The gradient of PN = 1 = m (2)
xx− 1

Equations (1) and (2) gives the same results.

( −
From equation (2), it implies that y − y = 1 mx x 1 ). Making y the subject gives
( −
y = mx x 1 ) + y 1
Further simplification gives y = mx mx− 1 + 1 . y

Rearrangement gives y mx= + (y − 1 mx 1 ). Mathematics Form One
Let c = y − mx 1 , it follows that y = mx + (y − 1 mx 1 ) is simplified to
1
y = mx c+ (3)

131

25/10/2024 09:51:49
Mathematics form 1.indd 131
Mathematics form 1.indd 131 25/10/2024 09:51:49