Page 132 - Mathematics

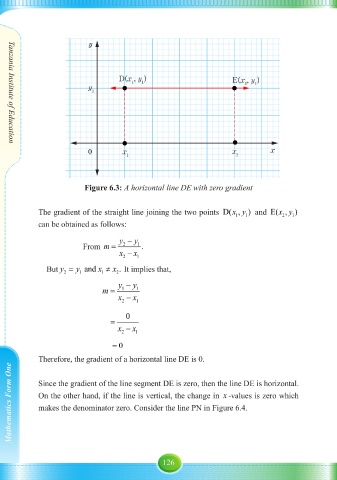
y

D(x , y ) E(x , y )
1
1
y 2 1
1

Tanzania Institute of Education
0 x x x
1 2

Figure 6.3: A horizontal line DE with zero gradient

The gradient of the straight line joining the two points D( , )xy and E( , )xy
1
2
1
1
can be obtained as follows:
y − y
From m = 2 1 .
x − x 1
2
But y = y 1 and x ≠ x 2 . It implies that,
2
1
y − y
m = 1 1
x − x 1
2
0
=
x − x 1
2
= 0
Therefore, the gradient of a horizontal line DE is 0.
Mathematics Form One Since the gradient of the line segment DE is zero, then the line DE is horizontal.

On the other hand, if the line is vertical, the change in x -values is zero which
makes the denominator zero. Consider the line PN in Figure 6.4.

126

25/10/2024 09:51:47
Mathematics form 1.indd 126
Mathematics form 1.indd 126 25/10/2024 09:51:47